Power of a Power Worksheet, Rules, and Definition

Get the free Power of a Power worksheet and other resources for teaching & understanding solving the Power of a Power

How to use the Power of a Power Rule for Exponents | Mathcation

Watch this video on YouTube



Key Points about the Power of a Power Rule

The power of a power rule simplifies expressions with exponents by multiplying the exponents.
The power of a power rule is a fundamental rule of exponents used extensively in higher-level math courses.
Understanding the power of a power rule is crucial for students learning algebra.

Power of a Power Rule for Exponents

There is a simply formula when using the Power Rule for simplifying exponents. In order to use the Power Rule for exponents, you keep the base of the power the same and you multiply the exponents. Always remember to be careful of the sign of the exponents.

The power of a power rule is an essential concept in algebra that simplifies expressions with exponents. It is a rule that is applied when a base is raised to a power, and then the whole expression is raised to another power. The power of a power rule states that when a power is raised to another power, you can multiply the exponents.

For example, 2 to the power of 3 raised to the power of 2 can be simplified as 2^(3*2) or 2^6 which equals 64. The power of a power rule is one of the fundamental rules of exponents, and it can help simplify complex expressions with ease.

Understanding the power of a power rule is crucial for students who are learning algebra, as it is used extensively in higher-level math courses. This article will explore the concept of the power of a power rule in detail, provide examples, and answer frequently asked questions.

Common Core Standard: 8.EE.A.1
Basic Topics:
Related Topics: Product Rule, Quotient Rule, Power of a Quotient Rule, Power of a Product Rule, Negative Exponents
Return To: Home, 8th Grade

What is the Power of a Power Rule?

The power of a power rule is a mathematical rule that simplifies expressions that involve raising a base to a power, and then raising the result to another power. In essence, it states that when a power is raised to another power, the exponents can be multiplied. This rule is an essential part of the algebraic toolkit and is used extensively in higher mathematics.

Application of the Rule

The power of a power rule is used in a variety of mathematical applications. For instance, it is used in the calculation of compound interest rates, where the interest rate is compounded over multiple periods. It is also used in the calculation of population growth rates, where the population grows exponentially over time.

In physics, the power of a power rule is used to calculate the energy of a system. For example, the kinetic energy of an object is calculated by raising its velocity to the power of two and multiplying it by its mass. The result is then divided by two.

Simplifying Expressions

The power of a power rule is also used to simplify expressions that involve exponents. For instance, if an expression has a base raised to a power, and this result is raised to another power, the exponents can be multiplied.

For example, consider the expression (2^3)^4. Using the power of a power rule, we can simplify this expression to 2^(3*4), which is equal to 2^12. This simplification is possible because the power of a power rule allows us to multiply the exponents.

In summary, the power of a power rule is a fundamental mathematical rule that simplifies expressions involving exponents. It is used in a variety of mathematical and scientific applications and is an essential part of the algebraic toolkit.

3 Simple Power of a Power Examples

The power of a power rule is an important concept in mathematics that helps simplify expressions with exponents. The rule states that if a power is being raised to another power, you can multiply the exponents and leave the base the same.

When using the Power of a Power Rule for Exponents you must multiply the exponents together.
You multiply whatever exponents is on the outside of the parenthesis to everything that is on the inside of the parenthesis.
When multiplying, make sure you include any negatives if there are any.

Here are some examples to illustrate the power of a power rule:

(a^2)^3 = a^(2*3) = a^6
(x^3)^4 = x^(3*4) = x^12
(5^4)^2 = 5^(4*2) = 5^8

In the first example, (a^2)^3 can be simplified by multiplying the exponents 2 and 3 to get 6 and leaving the base a the same. The result is a^6. Similarly, in the second example, (x^3)^4 can be simplified to x^12 by multiplying the exponents 3 and 4. In the third example, (5^4)^2 can be simplified to 5^8 by multiplying the exponents 4 and 2.

The power of a power rule can also be used to simplify expressions with variables and constants. For example:

(2x^3)^2 = 2^2 * (x^3)^2 = 4 * x^(3*2) = 4x^6
(3y^2)^3 = 3^3 * (y^2)^3 = 27 * y^(2*3) = 27y^6
(-4z^2)^4 = (-4)^4 * (z^2)^4 = 256 * z^(2*4) = 256z^8

In the first example, (2x^3)^2 can be simplified by first multiplying the constant 2^2 and then applying the power of a power rule to the variable x^3. The result is 4x^6. In the second example, (3y^2)^3 can be simplified by first multiplying the constant 3^3 and then applying the power of a power rule to the variable y^2. The result is 27y^6. In the third example, (-4z^2)^4 can be simplified by first multiplying the constant (-4)^4 and then applying the power of a power rule to the variable z^2. The result is 256z^8.

The power of a power rule can also be used to simplify expressions with fractions and negative exponents. For example:

(1/2^3)^2 = 1/2^(3*2) = 1/8
(1/x^-2)^3 = x^(2*3) = x^6
(5^-2)^3 = 5^(-2*3) = 1/125

In the first example, (1/2^3)^2 can be simplified by applying the power of a power rule to the denominator 2^3. The result is 1/8. In the second example, (1/x^-2)^3 can be simplified by applying the power of a power rule to the denominator x^-2. The result is x^6. In the third example, (5^-2)^3 can be simplified by applying the power of a power rule to the exponent -2. The result is 1/125.

Overall, the power of a power rule is a useful tool for simplifying expressions with exponents. Whether dealing with variables, constants, fractions, or negative exponents, the power of a power rule can help save time and effort in solving mathematical problems involving multiplication and division of powers.

5 Quick Power of a Power Practice Problems

Power of a Power Definition

The power of a power rule is a fundamental concept in mathematics that involves simplifying expressions with exponents. When a base is raised to a power, and then the whole expression is raised to another power, the power of a power rule states that the exponents can be multiplied.

For example, if a variable “x” is raised to the power of “m” and the whole expression is raised to the power of “n”, then the power of a power rule states that the result is x^(m*n).

This rule applies to positive exponents, negative exponents, negative numbers, and negative powers. When dealing with negative exponents, the power of a power rule can be used to convert them into positive exponents.

The power of a power rule can also be used to simplify expressions with negative numbers. For instance, (-2)^3 can be written as (-2)^2 * (-2), which is equal to 4 * (-2) = -8.

It is important to note that the power of a power rule only applies when the base is the same. If the bases are different, the expression cannot be simplified using this rule.

Overall, the power of a power rule is a crucial concept in algebra and calculus. It allows mathematicians to simplify complex expressions and solve equations more efficiently.

Power of a Power Rule FAQ

How do you simplify expressions using the power of a power rule?

To simplify an expression using the power of a power rule, you need to multiply the exponents. For example, if you have (x^2)^3, you can simplify it to x^(2*3) = x^6.

What is the power of a power property of exponents?

The power of a power property of exponents states that when you have an exponent raised to another exponent, you can multiply the exponents. For example, (x^2)^3 = x^(2*3) = x^6.

What is an example of applying the power of a power rule?

An example of applying the power of a power rule is simplifying (2^3)^2. You can rewrite it as 2^(3*2) = 2^6, which equals 64.

How do you simplify expressions using the power of a product rule?

To simplify an expression using the power of a product rule, you need to distribute the exponent to each factor. For example, (xy)^2 can be simplified to x^2y^2.

What is the quotient of a power rule?

The quotient of a power rule states that when you divide two powers with the same base, you can subtract the exponents. For example, x^5 / x^2 = x^(5-2) = x^3.

What is the fraction power to power rule?

The fraction power to power rule states that when you have a fraction raised to a power, you can raise both the numerator and the denominator to that power. For example, (1/2)^3 = 1^3 / 2^3 = 1/8.

What is the power of a power in math?

The power of a power in math refers to the property of exponents that allows you to simplify expressions with multiple exponents by multiplying them together. This property is useful in algebraic equations and calculus problems.

Power of a Power Rule Worksheet Video Explanation

Watch our free video on how to use Power of Power Rule of Exponents. This video shows how to solve problems that are on our free Power to a Power worksheet that you can get by submitting your email above.

Watch the free Power of a Power video on YouTube here: Power of a Power

Video Transcript:

This video is about the power rule exponents. You can get the power rule exponents worksheet we use in this video for free by clicking on the link in the description below.

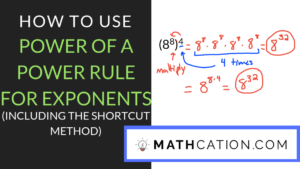
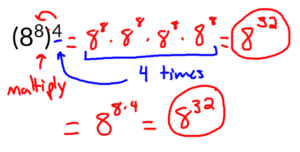
The first problem we’re going to work on on our power of a power rule of exponents worksheet is number two. This problem gives us 8 to the 8th raised to the 4th power. In order to simplify this problem you have to take the exponent that is on the outside of the parenthesis and distribute it to every exponent that is on the inside of the parenthesis. Now in the case of this example this is like saying we have 4 8 to the 8th powers. If we were to rewrite this we would rewrite it 8 to the eighth times itself 4 times.

We have our 8 to the 8th right now and we wrote it out four times because it is being raised to the exponent of 4. You should remember from the product rule for exponents that whenever you multiply exponential terms you keep the base the same and you add the exponents. If we look at this problem we will keep the base of 8 and then we’re going to add all of the exponents together. 8 plus 8 plus 8 plus 8 is 32, so our answer would be 8 to the 32nd power.

Now there is a shortcut for solving the power rule of exponents that you can do by skipping this middle step here. If you look at our original problem we have 8 to the 8th raised to the 4th power and if you look at our answer 8 to the 32nd power you might notice that if we had multiplied 8 times 4 we could get 32. So instead of having to write it out and add the exponents together. The shortcut for the power power rule for exponents is to do just that, it is to multiply.

In the case of this problem 8 to the 8th with raised to the 4th power you can do 8 to the 8 times 4 which would be 8 to the 32nd power. That’s the same answer we got in our first step. Now that we know the shortcut for the power to power rule we can go ahead and do a couple other practice problems.

In the case of this problem we have X to the 6 raised to the third power. I told you anytime you have a parenthesis in between two exponents that means you’re going to multiply the exponents. This is like saying X to the sixth times three. Which would be X to the 18th power and that’s going to be your answer.

This is the last problem we’re going to go over. This problem gives us negative exponents. We have 4 to the negative 2nd raised to the negative 2nd power. We already learned that anytime that there is a parenthesis in between two exponents that means to multiply so we’re going to keep the rule the same. Even though we have negative exponents we’re still going to multiply the two exponents together. Now the only trick when you have negative exponents is that you must include the negative when you multiply the exponents together. We will do negative 2 times negative 2 and when we do negative 2 times negative 2 you will get a positive 4. The solution is 4 to the positive fourth power.