Similar Figures Worksheet, Examples, and Definition

Similar Figures Definition

Similar figures refer to two-dimensional geometric shapes that have the same shape but may differ in size. In other words, similar figures have corresponding angles that are equal and corresponding sides that are proportional.

Proportion and Ratio

Proportion and ratio are essential concepts in understanding similar figures. Proportion refers to the equality of two ratios, while a ratio is a comparison of two quantities. In similar figures, corresponding sides are proportional, meaning that the ratio of the lengths of any two corresponding sides is the same.

Scale Factor

The scale factor is a ratio that compares the size of two similar figures. It is the ratio of any two corresponding lengths in the two figures. The scale factor can be used to find the missing side length or perimeter of a similar figure.

Corresponding Sides and Angles

Corresponding sides and angles are the sides and angles in one figure that are in the same position as the sides and angles in the other figure. In similar figures, corresponding angles are equal, and corresponding sides are proportional.

To determine if two figures are similar, it is necessary to check if their corresponding angles are equal and if their corresponding sides are proportional.

Overall, understanding the concept of similar figures is crucial in geometry. It allows for the comparison of different shapes and sizes, and it is useful in solving problems related to scaling and proportionality.

Congruent and Similar Figures

When studying geometry, it is important to understand the concepts of congruent and similar figures. Congruent figures are identical in both shape and size, while similar figures have the same shape but may differ in size.

Congruent Figures

Two figures are said to be congruent when they have the same shape and size. This means that all corresponding sides and angles are equal. Congruent figures can be moved, rotated, or reflected without changing their size or shape.

For example, if two triangles have the same angles and the same side lengths, they are congruent. Congruent figures are often denoted by the symbol ≅.

Similarity

Similar figures have the same shape but may differ in size. This means that all corresponding angles are equal, but the corresponding sides are proportional. Similar figures can be obtained from each other by scaling, which means multiplying the length of each side by the same factor.

For example, if two triangles have the same angles but different side lengths, they are similar. Similar figures are often denoted by the symbol ∼.

It is important to note that similarity does not necessarily imply congruence. Similar figures may have different sizes, while congruent figures must have the same size.

In summary, understanding congruent and similar figures is important in geometry. Congruent figures are identical in both shape and size, while similar figures have the same shape but may differ in size. Congruent figures can be moved, rotated, or reflected without changing their size or shape, while similar figures can be obtained from each other by scaling.

Similar Triangles

Similar triangles are two triangles that have the same shape but different sizes. The corresponding angles of similar triangles are equal, and the corresponding sides are proportional. For example, if triangle ABC is similar to triangle DEF, then:

• angle A is equal to angle D
• angle B is equal to angle E
• angle C is equal to angle F
• side AB is proportional to side DE
• side BC is proportional to side EF
• side AC is proportional to side DF

Similar Polygons

Similar polygons are two polygons that have the same shape but different sizes. The corresponding angles of similar polygons are equal, and the corresponding sides are proportional. For example, if polygon ABCD is similar to polygon EFGH, then:

• angle A is equal to angle E
• angle B is equal to angle F
• angle C is equal to angle G
• angle D is equal to angle H
• side AB is proportional to side EF
• side BC is proportional to side FG
• side CD is proportional to side GH
• side DA is proportional to side HE

Similar Circles

Similar circles are two circles that have the same shape but different sizes. The radius of similar circles is proportional to the diameter or circumference. For example, if circle A is similar to circle B, then:

• the ratio of the radius of circle A to the radius of circle B is constant
• the ratio of the diameter of circle A to the diameter of circle B is constant
• the ratio of the circumference of circle A to the circumference of circle B is constant

Similar Quadrilaterals

Similar quadrilaterals are two quadrilaterals that have the same shape but different sizes. The corresponding angles of similar quadrilaterals are equal, and the corresponding sides are proportional. For example, if quadrilateral ABCD is similar to quadrilateral EFGH, then:

• angle A is equal to angle E
• angle B is equal to angle F
• angle C is equal to angle G
• angle D is equal to angle H
• side AB is proportional to side EF
• side BC is proportional to side FG
• side CD is proportional to side GH
• side DA is proportional to side HE

Similar Rectangles

Similar rectangles are two rectangles that have the same shape but different sizes. The corresponding angles of similar rectangles are equal, and the corresponding sides are proportional. For example, if rectangle ABCD is similar to rectangle EFGH, then:

• angle A is equal to angle E
• angle B is equal to angle F
• angle C is equal to angle G
• angle D is equal to angle H
• side AB is proportional to side EF
• side BC is proportional to side FG
• side CD is proportional to side GH
• side DA is proportional to side HE

Similar Squares

Similar squares are two squares that have the same shape but different sizes. The corresponding angles of similar squares are equal, and the corresponding sides are proportional. For example, if square ABCD is similar to square EFGH, then:

• angle A is equal to angle E
• angle B is equal to angle F
• angle C is equal to angle G
• angle D is equal to angle H
• side AB is proportional to side EF
• side BC is proportional to side FG
• side CD is proportional to side GH
• side DA is proportional to side HE

In summary, similar figures are important in geometry because they allow us to compare and analyze different shapes and sizes. By understanding the properties and characteristics of similar figures, we can solve various geometric problems and applications.

Similar Figures Real Life Examples

Similar figures are not just mathematical concepts but also have practical applications in real life. In this section, we will explore how similar figures are present in photographs and line segments.

Photographs

Photographs are a great example of similar figures in real life. When a photograph is taken, the image captured is a similar figure of the actual object or person. The photograph has the same shape as the object or person, but the size may differ. For instance, a photograph of a person standing in front of a building will have the same shape as the person and building, but the size of the building in the photograph will be smaller than the actual building.

Line Segments

Line segments are another example of similar figures in real life. A line segment is a part of a line that has two endpoints. When two line segments have the same shape, they are considered similar figures. For instance, the sides of a rectangle are line segments that have the same shape. The length and width of the rectangle may differ, but the shape of the sides remains the same.

Line segments are also used in construction and architecture. When designing a building, architects use similar figures to ensure that the building is proportional and aesthetically pleasing. For example, the height of a building may be a multiple of its base length, ensuring that all line segments used in the construction are similar figures.

In conclusion, similar figures are present in real life, and their applications are not just limited to mathematics. Photographs and line segments are just two examples of how similar figures are used in everyday life. By understanding similar figures, we can appreciate the world around us and the mathematical principles that govern it.

How to Solve Similar Figures FAQ

What is the difference between similar and congruent figures?

Similar figures have the same shape but are not necessarily the same size, whereas congruent figures have the same shape and size. In other words, if you can resize one figure to make it the same size as the other, then they are congruent. If not, then they are similar.

How do you determine if two figures are similar?

Two figures are similar if their corresponding angles are congruent and their corresponding sides are proportional. This means that if you can match up the angles of one figure with the angles of the other, and the side lengths are in the same ratio, then the figures are similar.

What are some examples of similar figures?

Examples of similar figures include two triangles with the same angles but different side lengths, two circles with the same shape but different sizes, and two rectangles with the same shape but different dimensions.

What is the formula for finding corresponding sides of similar figures?

To find the length of a corresponding side in a pair of similar figures, you can use the formula:

corresponding side of larger figure / corresponding side of smaller figure = scale factor

The scale factor is the ratio of the corresponding side lengths of the two figures.

How do corresponding angles of similar figures compare?

The corresponding angles of similar figures are congruent, which means they have the same measure. This is a key property of similar figures.

What are some real-life applications of similar figures?

Similar figures are used in many real-life applications, such as map-making, architecture, and engineering. For example, architects use similar figures to design buildings that are proportional to their surroundings, while engineers use similar figures to design models of structures before building them.

What are two similar figures examples?

Two examples of similar figures are a small and large triangle with the same angles but different side lengths, and a small and large circle with the same shape but different sizes.

Similar Figures Worksheet Video Explanation

Watch our free video on how to solve Similar Figures. This video shows how to solve problems that are on our free Similar Figures worksheet that you can get by submitting your email above.
Watch the free Similar Figures video on YouTube here:Understanding Similar Figures

Video Transcript:
This video is about more practice with similar figures. You can get the similar figures word problems worksheet we use in this video for free by clicking on the link in the description below.

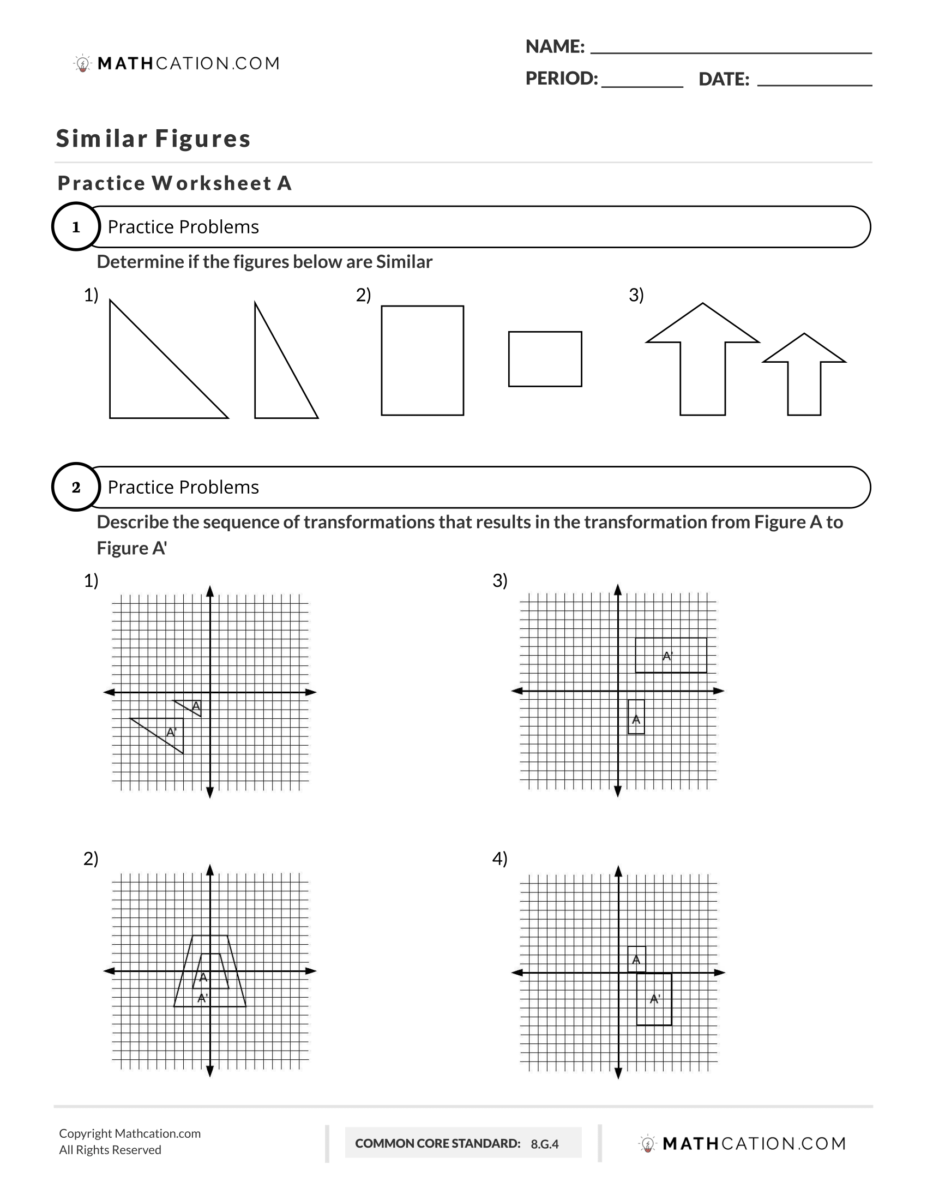
The first part of our similar figures worksheet asks us to determine if the figures below are similar. Now a similar figure is a figure that has the same shape but different sizes. When we say same shape that means that it has to have the same angles. For example, if we look at the first problem we’re given two triangles. Just because we’re given two triangles, which would technically be the same shape, the angles have to be the same. What that means is that they have to be the same exact figure, except the sizes are different.

If you look, these are the same shape but they may not have the same angles. If you look this angle in red and this angle in red, these are two different angles. This angle is wider than this angle and this angle in blue and this angle in blue are two different angles. This angle is wider than this one so that would mean that these shapes are not similar. We’re just going to write no.

Number two gives us two rectangles, which is the same shape. And then if you look, the rectangles have the same angle measures because they are all 90 degrees. These would be similar. And then number three these are two arrow is pointing straight up. Now these two arrows have different sizes. Obviously this arrow is larger than this arrow but they’re still the same shape which would mean that they are similar.

Part 2 of our similar figures worksheet asks us to describe the sequence of transformations that results in the transformation from figure a to figure a prime. What the phrase sequence of transformations means, means you have to describe how you can use translations, reflections, rotations, and dilations, to go from one figure to the other. In this case, to go from figure a to figure a prime.

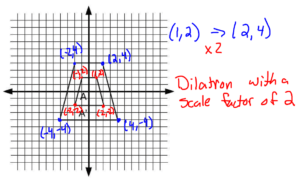
First problem we’re going to do on our similar figures worksheet is number two. The directions say that we have to figure out how we go from figure A, which is the smaller shape to the figure a prime, which is the larger shape. In this case, in order to do that the first thing I’m going to do label all the vertices and I’m also going to write the coordinates of those vertices.

If you look, the vertices here will be will say 1 X is 1 Y is 2, this vertices is X is 2 y is negative 2, this vertices X is negative 2 y is negative 2, and this vertice is X is negative 1 Y is 2. Then I’m going to label the vertices of a prime, which is the larger shape. This vertice is 2 4, this one is 4 negative 4, this one is negative 4 negative 4, and this one is negative 2 4.

Now that we have the vertices listed we can go ahead and make some assumptions about how we go from one to the next. Well if you look the shape gets larger or smaller which means it has to be a dilation. We have to use some type of dilation to go from one to the next now remember a dilation means you have to multiply the coordinates by a scale factor. In order to go from 1 2 into 2 4 we have to use a scale factor in the middle.

In this case what we did was we multiplied everything times 2. If you multiply all of your coordinates times 2 you will go from the inner shape into the outer shape. The series of transformations to go from figure a into figure a prime would be a dilation with a scale factor of two and that would be the answer.